How to Solve the Blockchain Trilemma: A BlockDAG and Nakamoto Consensus Friendship

Thesis: The blockchain trilemma claims that a network can only implement and maintain two of the three properties at any given time: decentralization, security, and scalability. Building upon Nakamoto Consensus through BlockDAG theory¹ solves the blockchain trilemma. Solving the trilemma implies two things, a) Satoshi’s peer-to-peer electronic cash system can be realized, and b) the most efficient layer-1 infrastructure can be created. Nakamoto Consensus alone cannot efficiently handle orphan blocks and is limited by a synchronous model, limiting its scalability and security. However, I will show how BlockDAG theory unlocks the full potential of Nakamoto Consensus.
Within this essay, I will explain 1) what Nakamoto Consensus is, 2) why it has difficulty scaling, and 3) how implementing BlockDAG technology scales Nakamoto Consensus. I will explain 3) by providing a history of BlockDAG theory. This history will primarily cover the following protocols: GHOST, Inclusive protocols, SPECTRE, PHANTOM, GHOSTDAG, and DAGKNIGHT. Lastly, I will conclude how BlockDAG theory fulfills the three properties of the blockchain trilemma for Nakamoto Consensus.
What is Nakamoto Consensus?
Nakamoto Consensus is a proof-of-work² consensus mechanism for the algorithmic ordering of a blockchain. Let’s cover some jargon: proof-of-work, blockchain, and algorithmic ordering. Cynthia Dwork and Moni Naor initially introduced proof-of-work in their work, Pricing via Processing or Combatting Junk Mail³, to combat Denial-of-service attacks; however, Nakamoto proof-of-work is primarily useful to combat Sybil attacks (an attack where one or a few gain disproportionate influence over decisions made in the network by obtaining an abundance of computing resources). To combat Sybil attacks, participants (otherwise known as miners) in a proof-of-work system solve challenging computational proofs to confirm blocks within the network (i.e., the confirmation of transactions) to receive a reward. Moreover, the nature of computation allows the network to quantify how much work a given proof contains.
Blockchains are distributed systems that are run in a decentralized manner by nodes that do not need to trust one another. These systems must agree on a history or state of the world through a consensus. Moreover, these consensus orderings must satisfy certain properties to obtain “correctness.” Nakamoto Consensus⁴ adopts the correctness theory proposed by Leslie Lamport in Proving the Correctness of Multiprocess Programs⁵. Lamport argued that both liveness and safety properties must apply to achieve correctness. Safety is the inability to revert a decision, while liveness is the inability to delay a decision.
Blockchains work according to a total ordering on which a miner appends an entry (otherwise known as a block of transactions) atop a previous entry known as a reference (previous block hash). Within a total order, events have an exact order based on which event occurred first, creating a chain.
Chains may also form natural forks where a second one-directional chain is built alongside the main chain. This happens when two miners create blocks at approximately the same time. When forks occur, the previous chain — known as an orphan chain — is no longer useful as the network decided to move forward with the new chain. Miners determine which blockchain to work on based on the Nakamoto consensus ordering algorithm, the longest chain rule. According to the longest chain rule (well, it actually works on a heaviest chain rule, but I am sweeping this detail under the rug for simplicity), miners must choose the chain that has computed the most-accumulated proof-of-work by analyzing the difficulties of each block in that specific blockchain (i.e., a more computational effort has been expended to verify and confirm blocks within the network on one chain than another). For simplicity’s sake, it’s assumed that the longest chain by height correlates to the longest chain by aggregate work/hashes computed.
It’s important to note that once a fork is resolved, transactions on the losing blockchain are invalidated unless they were simultaneously included in the winning blockchain.⁶ This wastes electricity and computational power and slows down the network.
The longest chain rule also adheres to a block delay, L, whereby L continuously updates to keep block arrivals (otherwise known as the block creation or confirmation time)⁷ in ~10 minutes. The combination of L and proof-of-works computational power fulfills liveness and safety, as network users can assume with high probability that it is infeasible to reverse transactions after some number of blocks. Thus, Bitcoin functions according to a synchronous model, which assumes an agreed global upper bound on the network delay.

The longest-chain rule, however, is vulnerable to history rewrites if an attacker mines a chain longer than the honest chain. A history rewrite (otherwise known as a reorganization or reorg) can be used for fraud — for example, let’s say that a participant, person A, purchases a rare guitar from another participant, person B, for 2 BTC. Person A sees the transaction is included in block D and, thus, hands over the guitar. However, person B decides to mine two consecutive blocks, E and F, on top of block C, using the same funds they used to buy the guitar to pay themselves. All miners will abandon block D and start extending block F due to the longest chain rule, and person A is left without 2 BTC and their guitar. This is called a double-spend attack.

Person A can protect themselves from such an attack by waiting for a few blocks after block D before they give person B the guitar, reducing the chance that person B will succeed in building a competing chain. Typically, a transaction is considered confirmed once six blocks have passed (resulting in a confirmation time of 60 minutes). This default time is based on the assumption, α, that an attacker has 10% of the network’s total hash rate and a risk, ε, of <0.1% a node is willing to absorb⁸. However, if person B has 51% of the mining power, they can implement a reorg regardless of how long person A waits. This is because person B’s block creation rate is higher than the other miners’ creation rates combined. Thus, proof-of-work systems assume that at least 50% of the honest mining power must belong to honest participants. More specifically, a 49% attack is prevented by math, and a 51% attack is prevented by money. The probability of a 49% attack to succeed decreases exponentially with the number of confirmations. A 51% attack has a chance to win if it can run long enough; however, the cost of such an attack is huge.
Why Chains Cannot Scale Nakamoto Consensus
In their paper, Secure High-Rate Transaction Processing in Bitcoin⁹, Yonatan Sompolinsky and Aviv Zohar proved how increasing Bitcoin’s throughput — either by increasing the block creation rate λ, or the block size, b — could reduce the 51% attack threshold to implement a reorg.
Increasing the block size. Sompolinsky and Zohar studied the work of Christian Decker and Roger Wattenhofer in Information Propagation in the Bitcoin Network¹⁰, taking a large sample of network nodes from height 180,000 to 190,000 of the public ledger. As shown below, it was discovered a linear relationship between block size and propagation time; the larger the block size, the longer the propagation time. The linear increase occurs because of the verification time — i.e., if a block is five times larger, it takes a node five times longer to verify the block before rebroadcasting it.

For example, let’s say the Bitcoin community wants to scale the network to Visa levels to process 2,000 transactions per second. Bitcoin’s current throughput is about 7 transactions per second due its current block size of 2 MBs. Thus, Visa levels would require a block size 285 times larger, equalling 570 MBs. With a network delay of 285 seconds (assuming the network delay is linear) and a block creation rate of one block every 600 seconds (10 minutes), there is a 285/600=0.475 chance that another block will be created — meaning almost 50% of the blocks will belong to forks. This allows an attacker to maintain a reorg attack simply by creating blocks faster than the main chain.
Increasing the block creation rate. Bitcoin’s network delay is about 1 second, and as we know, a new block is created on average every 600 seconds (10 minutes). Because the average block’s creation time is 600 times bigger than the network delay, it’s improbable that a block will be mined while another block is still propagated.¹¹ However, the likelihood increases once the block creation rate increases. If the block creation rate increases, more blocks will be created while the most recent block in the main chain is propagated. This will cause more forks as the likelihood of every miner not being up to date will also increase. Similarly, as in the case of increasing block sizes, attackers can execute reorg attacks by creating blocks faster than the main chain with less than 51% hash power, as shown in the illustration below.

When an attacker sees a fork trying to be resolved (causing a temporary slowdown of the main chain), the attacker will use that time to outrun the main chain to create a longer chain (known as selfish mining)¹². The longer chain will start as a secret chain until it’s long enough to be announced and adopted by the other miners. Moreover, the attacker can do this with less than 51% of the hash power. Why? Because if half of the blocks are forked, only two-thirds of them will go into the main chain — meaning an attacker only needs 50%×(2/3)=33% of the hashing power to sustain an attack. Moreover, electricity and computational costs are more significantly wasted, increasing the cost for new miners to enter the network and, thus, causing further centralization.
A Predecessor to BlockDAG: GHOST
GHOST (The Greedy Heaviest-Observed Sub-Tree)¹³ paved the way for BlockDAGs, as it resolved forking conflicts by using forks for the protocol’s advantage — thereby increasing throughput and security, as attackers can no longer outpace the network. The topology of Nakamoto Consensus changes with GHOST as aggregate work is viewed with a 2-dimensional view instead of a 1-dimensional view via tree graphs.¹⁴
Instead of following the longest rule at each fork, GHOST proposes to follow the heaviest subtree. In other words, the protocol will follow the path of a subtree with the combined hardest proof-of-work or difficulty.
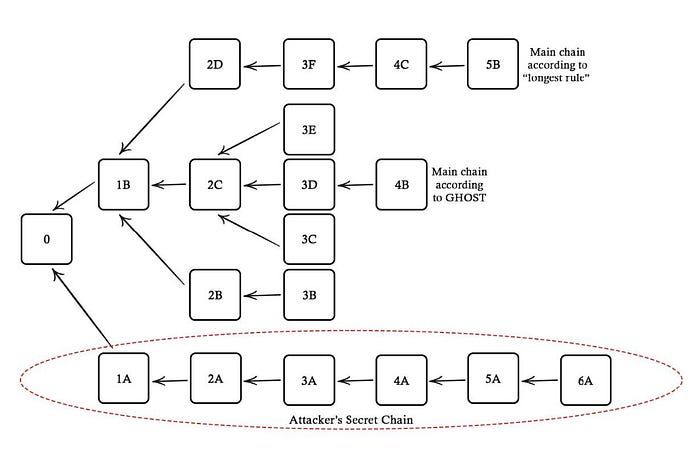
Let’s take a look at the following illustration above. As we can see, multiple forks have been generated alongside the main chain (either by increasing the block creation rate or size); by the second layer, there is a three-pronged fork, and another by the 3rd layer. The attacker’s chain (6 blocks) is longer than the main chain of the network ending in 5B and would assume the place of the main chain under the longest-chain rule. However, under GHOST, the main chain selected is the one with the most combined work.
Thus, GHOST considers all blocks within the network and incorporates forked blocks within the main chain; this saves electricity and computational power and also increases throughput as the block creation rate or size can increase without harming security. Sompolinsky and Zohar provided data to demonstrate this, by simulating the network with 1,000 nodes according to several uniform parameters. As the block creation rate increases, security remains constant for blockchains.

Ethereum, as a proof-of-work blockchain, was able to increase its throughput higher than Bitcoin (roughly 20 transactions-per-second compared to Bitcoin’s 7 transactions-per-second) and decrease wastage by implementing a variant of GHOST, as an inclusive protocol, from the work, Inclusive Block Chain Protocols, by Yoad Lewenberg, Yonatan Sompolinsky, and Aviv Zohar.¹⁵
In an Inclusive protocol, the following properties are obtained: (1) new blocks reference multiple predecessors; (2) non-conflicting transactions within blocks outside of the main chain are included in the ledger; and (3) miners of blocks outside the main chain receive a portion of the block reward. Within Ethereum, however, transactions in referenced forked blocks are not included in the ledger, and miners of these transactions do not receive transaction fees. Only referenced orphan block (otherwise called Ommer blocks) miners receive a portion of the block reward.¹⁶
However, while GHOST made headway to increase the scalability and security on top of Nakamoto-generalized protocols, it still had its flaws. First, improved security comes at the expense of slightly slower time resolving forks; for example, GHOST couldn’t scale to, say, 1 second blocks. Or it can be said that the more “inclusive” you are (in the sense of how distant a cousin has to be from the main chain to be included), the worse your confirmation times become. Secondly, miners who are better connected to the network could gain rewards greater than their fair share. Lastly, the ability to form secret chains still remains possible with selfish mining.
SPECTRE
GHOST introduced graph theory with subtrees¹⁷ as a generalized Nakamoto Consensus mechanism. SPECTRE¹⁸ took the idea further by implementing a full BlockDAG to build upon Nakamoto generalization. In other words, in GHOST, trees were leveraged to solve Nakamoto’s orphan rate problem, and SPECTRE leverages a BlockDAG to solve the orphan rate problem. Moreover, SPECTRE provides greater scalability than GHOST or basic Nakamoto Consensus by implementing weak liveness.
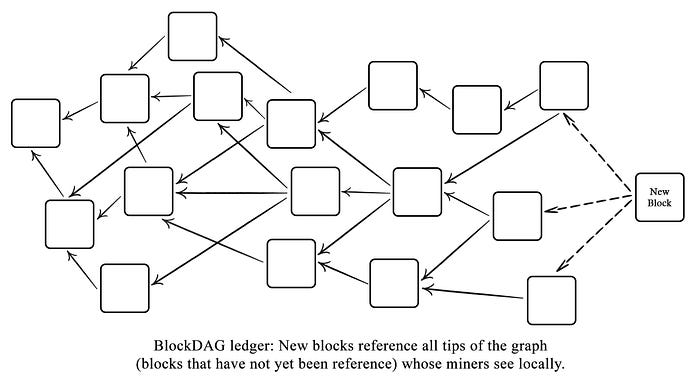
What is a BlockDAG? DAG stands for direct acrylic graph; meaning (1) it is a data structure moving in one direction; (2) the data structure is non-cyclical, and therefore cannot return to a previous state from the current state; and (3) it is structured as a graph, G=(V, E), with vertices and edges. In typical DAG structures, transactions are documented as vertices without the implementation of blocks, and edges provide direction for each vertex. However, vertices within BlockDAGs are blocks, which reference multiple predecessor blocks (or parent blocks) instead of a single predecessor. In other words, to extend the ledger within a BlockDAG, blocks reference all tips of the graph (that their miners observe locally) instead of referencing the tip of the single longest chain. A DAG built of blocks decreases the forking dilemma of Nakamoto Consensus, as the main chain can now point to forked blocks; more so, work is no longer discarded when facing an attacker.
The topology of a BlockDAG is such that if U and V are connected by the edge e=(U →V), U comes before V in the ordering, O. In other words, if a path exists from block V to block U in the DAG, block U was created before block V and should precede V in the global order. However, a defined ordering is needed when blocks are created in parallel — i.e., a set of blocks without a path connecting them, as in the case of forks. This is where SPECTRE comes in. SPECTRE is an ordering algorithm that eliminates transactions in conflict with previous ones.
SPECTRE’s ordering is conducted through a pairwise voting mechanism to determine how likely transactions will be reversed. For each pair of blocks U, V, a vote must determine whether U defeats V or V defeats U, denoted by U>V or V>U. Moreover, within a set of transactions, a transaction embedded in U is accepted if block U defeats all blocks containing conflicting transactions¹⁹. This is quite abstract; let’s break it down. First, “defeat,” denoted as U>V, does not mean one block is greater than the other. Rather it means one comes before the other, i.e., U comes before V. Furthermore, defeating one block with another only matters if conflicting transactions are present between the two; otherwise, non-conflicting transactions will always be accepted.
Voting is conducted by the blocks themselves (the determiners). There are three ways a block, Z, may conduct a vote: (1) if block V has a path back to U, then Z will vote U>V; (2) if there is no path between block V and U, Z will vote for the block within its local ordering it can see — so if Z sees U but not V, then U>V; (3) if there is no path between V and U and Z sees both U and V, then it’ll vote according to a recursive computation based on how other past blocks have voted. For example, Block 12 (in the image below²⁰) votes for an ordering that does not contain blocks 10,11, and 12 because more blocks voted for X>Y in 12’s past than 9–10–11’s voted for Y>X. This is a generalization of the longest chain rule, as the path chosen is the path with the most votes.

SPECTRE’s Weak Liveness. Unlike Bitcoin and other Nakamoto generalizations covered, SPECTRE is agnostic to the network’s global network delay, D. An upper bound of D is assumed; however, the bound is assumed locally by each node, which each node can adjust as network conditions change. This allows SPECTRE to achieve fast confirmation times during healthy periods and maintain responsiveness during network conflicts. In this positive sense, this is also known as a parameterless model; however, “self-scaling” is better term. Moreover, each node is responsible for its choice in D, as an overly inaccurate choice can harm them. For example, if a node overestimates D, it cannot recognize an irreversible transaction, and if a node underestimates D, it will accept transactions prematurely.
Liveliness is therefore weakened; however, it is only weakened when conflicting transactions occur. In other words, as long as there are no conflicting blocks, ordering doesn’t matter. The “voting” mechanism kicks in only if a conflict is detected. For example, if a published transaction with zero published conflicts is guaranteed irreversibility very quickly. However, suppose two or more conflicting transactions are published simultaneously or soon after one another. In that case, their irreversibility will be decided on within a longer finite time frame. This allows a significant increase in throughput.
Nonetheless, it’s important to note that SPECTRE was designed solely for payment use cases, whereby the owner of the funds functions as the sole entity to produce and sign transactions (including conflicting ones). SPECTRE’s pairwise ordering is not transitive²¹ and, thus, does not provide a linear ordering, as blocks can switch places long after being confirmed (without invalidating transactions). This does not work for smart contracts as strict ordering among transactions is required; otherwise, having out-of-order computations can cause some to fail, and users could feed the contracts with conflicting inputs. With this in mind, GHOSTDAG was designed to support smart contacts by implementing a converging linear ordering.
PHANTOM and GHOSTDAG
GHOSTDAG implements a total ordering, allowing the ability to develop smart contracts atop the protocol as computation will occur in exactly the way the designer intended. The trade-off is that GhostDAG implements an upper bound on the network latency time, and is thus, non-responsive to network latency. GHOSTDAG is built upon the foundations of PHANTOM in PHANTOM GHOSTDAG: A Scalable Generalization of Nakamoto Consensus by Yonatan Sompolinsky, Shai Wyborski, and Aviv Zohar.²²
PHANTOM. PHANTOM is a blockDAG ordering algorithm constructed theoretically without real-world efficiency in mind. PHANTOM’s goal is to order honest blocks in a well-connected manner. Since honest nodes aren’t withholding blocks and communicating with one another, their computational work should be well connected. On the other hand, an attacker developing a secret side chain would be disconnected from the main chain. In a typical BlockDAG, each block references all blocks known to its miner when it was created, but how do we know which blocks are well-connected and which aren’t?
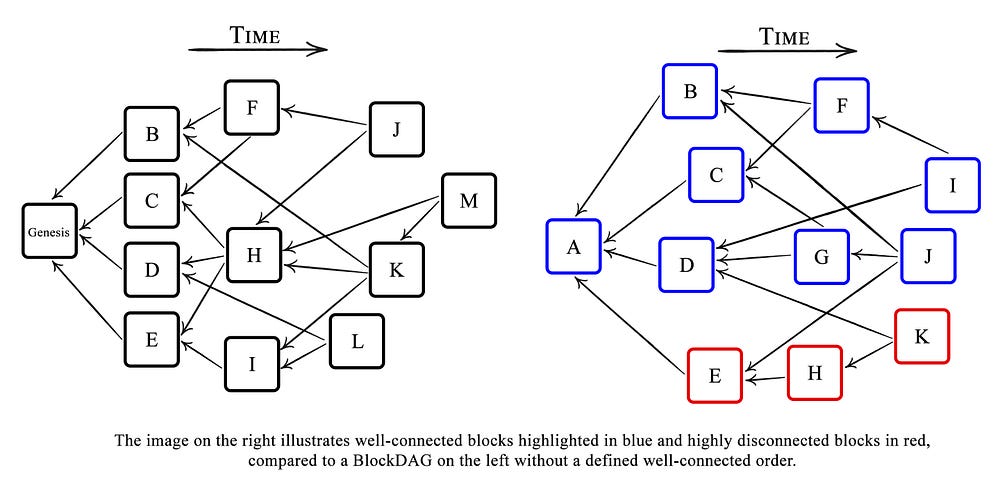
From a single block’s perspective, B, a BlockDAG is divided into three subsets: the block’s past (the set of blocks reachable from B), future (the set of all blocks from which B is reachable (equivalently the set of all blocks which have B in their past), and the block’s anticone. Anticones are blocks that are neither a block’s past nor future. The well-connected set is the biggest sub-DAG (otherwise known as a K-cluster) where no block has an anticone greater than K. In other words, the PHANTOM optimization rule always returns a max K-connected cluster, such that a tie-breaking rule is implemented if there are several maximal K-clusters.
K represents the maximum antigone size within a K-cluster, and K must be greater than 2Dλ, whereby D equals the network delay and λ equals the block creation rate. K is hard coded in PHANTOM (and GHOSTDAG) and is, thus, selected in a predetermined manner. Therefore, deciding the value of K is very important. If the value of K is too large, too many forks will occur, reducing the network’s security; if the value of K is too small, it will limit the network’s performance, lowering the throughput.

For example, if we look at the well-connected blocks highlighted in blue in the diagram above (with K=3), we can now identify that each blue block has at most 3 blue blocks in its anticone. Thus, at most, 4 blocks are assumed to be created within each unit of delay, and the anticone size should not exceed 3. Therefore, blocks outside the cluster, E, H, and K (colored red), belong to the attacker. For instance, block E has 6 blue blocks in its anticone (B, C, D, F, G, and I), as these blocks didn’t reference E (as E was likely withheld from its miners). Similarly, block K has 6 blue blocks in its anticone (B, C, G, F, I, and J).
However, finding a maximal K-cluster is NP-hard, meaning that the likelihood of proving it will result in the breakdown of what we know about computer science. Moreover, PHANTOM does not work in an incremental manner; whenever the DAG updates, the entire computation must be restarted — requiring the storage of the entire DAG structure.
GHOSTDAG and its Linear Ordering. GHOSTDAG functions as a greedy variant of PHANTOM, allowing a practical approach for adoption. A greedy variant is an algorithm that solves a problem by making the locally optimal choice at each process stage. Thus, instead of finding a maximal K-connected cluster, GHOSTDAG approximates K incrementally and recursively. It does this by numbering each block with a blue score, indicating how many blocks in its past are in the K-cluster.²³
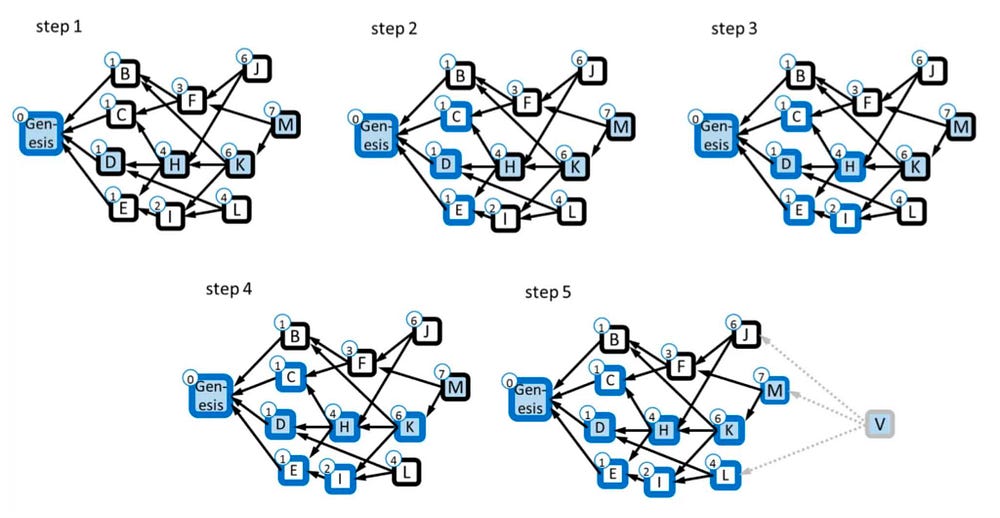
For example, if we look at Figure 3 from the PHANTOM GHOSTDAG paper, we can see how block M is recursively selected within a given K-cluster, G, with K=3. The circled number is the score of blue blocks in the DAG’s past. The GHOSTDAG algorithm greedily selects a chain starting from the highest scoring tip, M, and then K, as K is the highest scoring tip in M’s past (and then H, and D — D is arbitrarily selected to break the tie between C, D, and E — and lastly, the genesis). This chain is used to construct the blue block set of the DAG.
In step 1, while visiting D, the genesis block is added to the blue set since it is the only block in D’s past. In step 2, H is visited, and the blue blocks in its past — C, D, and E — are added. In step 3, K is visited with the blocks of its past — H and I — added. However, block B is not added to the overall blue set because it has an anticone of 4. In step 4, M is visited with K added to the blue set. F was not added due to its large anticone. In the last step, 5, a hypothetical block, V, is visited, (whose past equals the DAG) with M added to the blue set. Block L and J are left out as L has a large anticone and because adding J would increase the anticone of L even more.
However, what happens when an attacker allows their blocks to point to honest blocks to increase their blue score? GHOSTDAG implements a mechanism to stop this, known as the freeloading bound. The bound mechanism ensures that a miner can only freeload older blocks by a specific constant (namely 3k+1 blocks). Thus, changing the ordering of arbitrarily old blocks will run into a race where freeloading does not provide the attacker any advantage over honest nodes who consistently point to other honest blocks.
GHOSTDAG Issues Resolved by DAGKNIGHT
GHOSTDAG affords nearly immediate confirmation times (in the order of seconds). For example, Kaspa, built according to GHOSTDAG, achieves 10 blocks per second, or roughly 3,000 transactions per second.²⁴
However, It’s important to note that while a maximum K-cluster is not calculated in GHOSTDAG, parameter D is still chosen in advance — thereby assuming an a priori bound on the worst-case latency.²⁵ Thus, the BlockDAG under GHOSTDAG functions synchronously, meaning that there exists some known finite time bound Δ, whereby with any message sent, an adversary can delay its delivery by at most Δ. Moreover, setting an upper delay bound leads to a margin of error to maintain security, meaning two things:
(A) If latency improves below D, the confirmation time becomes suboptimal.
(B) If latency degrades above D, security will degrade with it.
For example, GHOSTDAG’s upper delay bound is set to 10 seconds, thus, given (A) and (B), if latency increases to 12 seconds for a period, a 45% attacker could take over the network; if latency increases to 60 seconds, a 25% attacker could take over the network. It’s important to note that this holds for all PoW chains.
DAGKNIGHT is a BlockDAG ordering algorithm written by Michael Sutton and Yonatan Sompolinsky in their work, The DAG KNIGHT Protocol: A Parameterless Generalization of Nakamoto Consensus.²⁶ DAGKNIGHT solves GHOSTDAG’s issues by designing a version of GHOSTDAG (maintaining its strong liveness) in a parameterless way by monitoring network conditions to determine the best current K and D.²⁷ In other words, instead of guaranteeing a 10-second confirmation delay, the confirmation time adapts automatically according to miner network conditions and optimizations in the block validation algorithm.
How does DAGKNIGHT do this? First off, it’s important to note that DAGKNIGHT is a greedy iteration of PHANTOM-X,²⁸ a term only known within the DAGKNIGHT research circle (i.e., the term doesn’t exist within the DAGKNIGHT paper). Instead of choosing K in advance, PHANTOM-X looks for the smallest K such that the largest K-cluster covers more than half of the blocks while maintaining 50% fault tolerance.
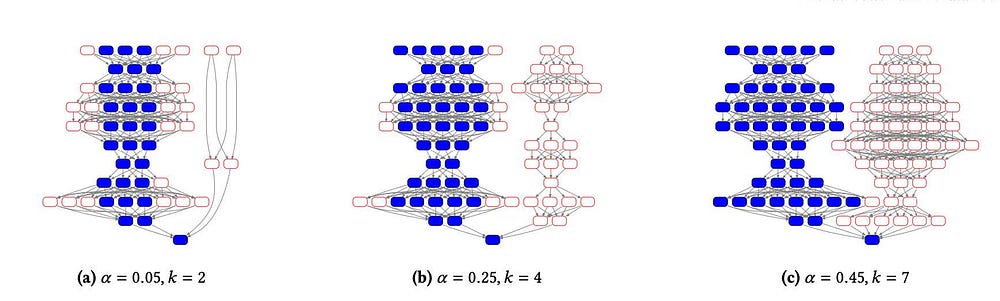
For example, as shown in the image below,²⁹ as an attackers fraction (on the right side of [a],[b], and [c]) grows from 𝛼 = 0.05 in (a) to 𝛼 = 0.45 in (c), the PHANTOM-X algorithm finds a K-cluster of sufficient width to cover at least 50% of the DAG, thereby outweighing the minority attacker.
Moreover, as shown in the second image below,³⁰ confirmation times change according to various network conditions. For example, as latency begins at 2 seconds per block in (a) and decreases to 0.1 seconds in (c), K decreases from 4 in (a) to 0 in (c). The confirmation time decreases from 12 seconds in (a) to 1.2 seconds in (c)while covering 50% of the DAG — demonstrating that confirmation times of PHANTOM-X change according to various network conditions while maintaining a security threshold of 50%.

In other words, PHANTOM finds a maximal k-cluster, which is NP impossible; so, a greedy variant was created, GHOTSDAG. Similarly, the PHANTOM-X solves the harder problem of a minimal maximal k-cluster (the minimal k such that the maximal k-cluster is at least half of the DAG). Therefore, DAGKNIGHT was created to follow a greedy variant of PHANTOM-X to recursively find a K-cluster of sufficient width to cover at least 50% of the DAG. The greediness (or, more accurately, “incrementality”) is *required* for establishing security: without it, the protocol cannot promise that the maximal K-cluster computed at some times doesn’t exclude blocks in earlier K-clusters.
DAGKNIGHT’s incrementality can resist 50% attacks without relying on network latency assumptions. Therefore, a margin of error is not required because if network conditions degrade, confirmation times will automatically increase to compensate. Moreover, this allows DAGKNIGHT to adjust block confirmation times according to real-time network conditions. For example, when the network’s adversarial latency is low, DAGKNIGHT’s orderings converge immediately, allowing clients to confirm transactions within a few Round Trip Times. On the other hand, when the network is slow and clogged, the orderings converge more slowly, and thus, allow the transaction confirmations to take longer.
It’s important to note that the parameterlessness property of DAGKNIGHT also holds for SPECTER; however, it comes at the cost of only having weak liveness (prohibiting the implementation of smart contracts). DAGKNIGHT, on the other hand, achieves BOTH parameterlessness AND strong liveness — and is the first protocol to do so.
Conclusion: How The Blockchain Trilemma is Solved
Some may argue that Nakamoto Consensus, namely the Bitcoin protocol, doesn’t need to scale, as the cryptocurrency is meant to be held as a store of value. This argument is not ridiculous, as it serves as an alternative to gold and silver. Nonetheless, if we want to fulfill Satoshi’s vision of a peer-to-peer electronic cash system, it must scale, as nobody will want to wait once 6 blocks have passed (60 minutes) to purchase something.³¹ Moreover, it has been shown that original Nakamoto Consensus cannot scale due to its synchronous nature and its conflicts arising from forks. However, it has been shown that generalized Nakamoto Consensus can- i.e., the BlockDAG protocols summarized above, namely GHOST, SPECTRE, GHOSTDAG, and DAGKNIGHT.
One may ask, why keep proof-of-work and mining to (a) fulfill Satoshi’s payment vision and (b) develop a layer 1 blockchain? Or more importantly, why solve the blockchain trilemma using generalized Nakamoto Consensus (as solving the blockchain trilemma achieves both [a] and [b])? The answer is that generalized Nakamoto Consensus achieves high levels of decentralization and security, especially compared to proof-of-stake and other Byzantine Fault Tolerant protocols. What original Nakamoto Consensus lacked was scalability. It’s already been shown that generalized Nakamoto Consensus is scalable. Therefore, if we can demonstrate that generalized Nakamoto Consensus, namely BlockDAG theory, is decentralized and secure, we can solve the blockchain trilemma.
Decentralization. Nakamoto Consensus is decentralized because miners within proof-of-work must continuously invest in order to maintain their relative power. This supports (1) economic decentralization and (2) a more permissionless system. Why is this the case? Let’s explain (1) and (2) by comparing proof-of-work to proof-of-stake. In proof-of-stake, staked participants do not need to continually invest in order to secure the network. Instead, already powerful nodes can gain more power since staked currency produces more currency from network rewards — empowering large stakeholders. This means there can be only one type of node on the network — a rich one. In contrast, miners within proof-of-work must update their hardware, maintain stable electrical costs, and ensure external factors do not interfere with production (i.e., storage, housing, and so on). For (2), anyone can provide proof-of-work and try to produce a block within the main chain. However, in proof-of-stake, users must either be a rich node or delegate their stake to the rich nodes, increasing the barrier of entry to participate in the network’s security and operations.
But what about other DAGS? Why focus on BlockDAG innovations? Many DAGS, such as IOTA, Byteball, and Nano, are blockless DAGs. Blockless is a fancy term for blocks with one transaction. Blocks with one transaction are not scalable. It is a “feature” which disables economies of scale, as users can no longer delegate their transactions to service providers to aggregate transactions. DAGs of this nature also rely on centralized authorities such as Coordinators double-checking all transactions, and thus, create a single point of failure.
Moreover, many blockchains utilize DAGs to process their transactions but not their ledgers (i.e., they are not a true DAG-based ledger). Blockchains within this camp include Fantom and Aleph Zero. On the other hand, current projects utilizing a DAG ledger operate according to proof-of-stake; thus, they are less secure, with a security threshold of 33% compared to 50%. These projects include Avalanche X-Chain and SUI.³²
Security. Nakamoto Consensus is secure as it has a security threshold of 50%, meaning that an attacker must have at least 51% of the network’s hash power to overcome the network. A security threshold of 50% is the highest security threshold modern-day cryptography can achieve, compared to Byzantine Fault Tolerant and proof-of-stake protocols, which are only resilient to an attacker achieving 33% of the network’s economic power. Moreover, BlockDAG Nakamoto generalizations significantly increase original Nakamoto security by solving conflicts arising from forks and hardwired upper bounds on network delays. Moreover, Nakamoto Consensus’ security exists within its own protocol and outside global forces. This is because proof-of-work creates harder, sounder money, as its value is anchored to markets beyond itself and an objective, physical grounding, such as electricity, computing hardware, and warehouses situated across the globe.
Some criticize proof-of-work’s reliance on electricity as a possible security concern (not to mention a burden to the environment). This is a justified concern, but current research in Optical-Proof-of-Work (otherwise called oPoW) alleviates this concern.³³ oPoW is a paradigm shift to lower operational costs (such as electricity), known as OpEx, to allocate more funds to capital expenses, known as CapEx. The desire to decrease operational costs reduces proof-of-work’s environmental impact and provides better network security. This is because an OpEx-heavy paradigm equates to miners burning the security budget by using it. Moreover, only countries with lower OpEx costs, such as electricity costs, can support proof-of-work infrastructure, thus severely increasing the barrier to entry.
Being CapEx-heavy, on the other hand, means the miner’s investment protects the system by locking them into the system without burning their investment with every new block mined. Moreover, a larger cache of specialized security hardware is maintained, increasing the barrier to attack. oPow, therefore, utilizes Optical ASICS, which uses very little energy to run. Optical technology has been widely adopted for AI servers and is compatible with the hashing algorithm, the kHeavyHash, utilized by GHOSTDAG and DAGKNIGHT.
It’s important to note that a CapEx paradigm does not mean it’s better to have higher CapEx costs; instead, miners can focus less on operational costs. For example, the cost of entering oPoW hardware manufacturing could be much lower³⁴ than ASICs since old Silicon Photonics, such as CMOS nodes (~90 or 220 nm vs. ~7 nm for transistors), are sufficient to create Optical ASIC mining hardware.
Some may argue that ASIC mining increases centralization due to their hash power dominance over GPUs and CPUs. However, fewer entities dominating the mining industry is not, in-and-of-itself, centralization, — as the entities cannot impose non-linear “rich-get-richer effects.” This was proven in Theorem 4 for original Nakamoto Consensus in the work Bitcoin Mining Pools: A Cooperative Game Theoretic Analysis.³⁵
Scalability. Nakamoto Consensus’s full potential is unlocked when it is discovered how to build it without scalability limitations, as scalability solutions simultaneously increase security. It started with GHOST utilizing subtrees to develop the heaviest chain rule to handle forking conflicts arising from the longest chain rule. However, GHOST’s security came at the expense of disallowing higher speeds; for example, GHOST cannot scale to 1-second blocks. Moreover, GHOST was still susceptible to secret chain attacks. GHOST’s speed was increased with SPECTRE utilizing BlockDAG technology and a partially synchronous model, achieving 10 blocks per second. SPECTRE is also capable of outrunning secret chain attacks.
Nonetheless, SPECTRE doesn’t implement linear ordering, a property necessary for building smart contracts. GHOSTDAG resolved this issue by implementing linear ordering while maintaining strong liveness; however, linear ordering came at the expense of implementing an upper bound on the network latency time. Thus, GHOSTDAG is non-responsive to network latency, causing security vulnerabilities. DAGKNIGHT solved GHOSTDAG’s security issues by designing a parameterless version of GHOSTDAG — merging useful properties from SPECTRE and GHOSTDAG into one protocol. Nonetheless, GHOSTDAG can reach throughput levels equivalent to Visa with 3,000 transactions per second, and with DAGKNIGHT, it can do so securely.
Conclusion. BlockDAG theory, as a generalization of Nakamoto Consensus, therefore, achieves high scalability. Even more so, scalability is achieved while increasing the security of original Nakamoto Consensus and maintaining its decentralization. Thus, we can say the blockchain trilemma is solved.
References and Footnotes
[1] More specifically, BlockDAG theory as a generalization of Nakamoto Consensus. The goal of generalization is to preserve the key aspects of Nakamoto Consensus while also implementing new structures to increase scalability, security, or decentralization. The BlockDAG theories covered in this essay are all generalizations of Nakamoto Consensus. Moreover, it’s important to note that I will cover how the blockchain trilemma is theoretically solved at the consensus level.
[2] Original Proof-of-stake (PoS) algorithms were based on Nakamoto Consensus; however, Nakamoto PoS, in its naive form, suffers from the “nothing at stake” problem and long-range attacks. Due to this issue, PoS systems adopted Byzantine Fault Tolerant-style consensus, known as state-machine-replication-based PoS. For this essay, I cover PoW-style Nakamoto Consensus only.
[3] Dwork, Cynthia, and Moni Naor. Pricing via Processing or Combatting Junk Mail, 1993, www.wisdom.weizmann.ac.il/~naor/PAPERS/pvp.pdf.
[4] Nakamoto, Satoshi. Bitcoin: A Peer-to-Peer Electronic Cash System, bitcoin.org/bitcoin.pdf.
[5] Lamport, Leslie. “Proving the Correctness of Multiprocess Programs.” IEEE Transactions on Software Engineering, Vol. SE-3, №2 , Mar. 1977, https://lamport.azurewebsites.net/pubs proving.pdf.
Other correctness theories have been proposed, such as FLP Impossibility and the CAP Theorem. FLP Impossibility was proposed by Fischer, Lynch, and Paterson, who described in their 1985 paper, Impossibility of Distributed Consensus with One Faulty Process, that liveness and safety cannot be satisfied in asynchronous distributed systems. The CAP theorem by Eric Brewer extended the work of FLP Impossibility.
[6] The invalidated transactions are re-included into a pool for future block inclusion of the correct blockchain. The excluded transactions can be automatically retransmitted and eventually be automatically included in the winning chain. For this reason, Bitcoin implemented a “coinbase cooldown,” whereby miners must wait for 100 blocks before they can spend block rewards — thus, block rewards can *not* be retransmitted, and they become invalid in a reorg.
[7] In other words, when transactions within a block are considered to be ‘processed.’
Moreover, the entire blockchain scalability problem can be reduced to the statement that “For a blockchain to be secure it must hold that D<<L” (<< means “much smaller”), whereby D = the network delay and L = the block delay.
[8] Rosenfeld, Meni. Analysis of Hashrate-Based Double-Spending, 11 Dec. 2012, bitcoil.co.il/Doublespend.pdf.
[9] Sompolinsky, Yonatan, and Aviv Zohar. Secure High-Rate Transaction Processing in Bitcoin, 2014, eprint.iacr.org/2013/881.pdf.
[10] Decker, Christian, and Roger Wattenhofer. “Information Propagation in the Bitcoin Network.” 13th IEEE International Conference on Peer-to Peer Computing, https://www.dpss.inesc id.pt/~ler/docencia/rcs1314/papers/P2P2013_041.pdf.
[11] The network delay is the time it takes for a block to be known by all miners, and as we know, the block creation rate is the time it takes for transactions within a block to be considered ‘processed.’
[12] Eyal, Ittay, and Emin Gun Sirer. Majority Is Not Enough: Bitcoin Mining Is Vulnerable, 2013, www.cs.cornell.edu/~ie53/publications/btcProcFC.pdf.
[13] Proposed by Yonatan Sompolinsky and Aviv Zohar in their work, Secure High-Rate Transaction Processing in Bitcoin.
[14] A graph network, G=(V, E) — whereby V = vertices and E = edges, has the following properties: (1) nodes function as vertices and edges function as peer connectors; (2) nodes have a fraction of the total computing power; (3), each edge has a time delay; and (4) blocks are generated via a Poisson process. Liveness is satisfied via proof-of-work, and safety is fulfilled as the network has a bounded upper delay, denoted by the sum of all individual node delays.
[15] Buterin, Vitalik. Ethereum Whitepaper, 2013, ethereum.org/en/whitepaper/.
Another idea that GHOST and the Inclusive protocol framework inspired was FruitChains: A Fair Blockchain, written by Rafael Pass and Elaine Shi. These two people also influenced the work of DAGKNIGHT with their work on synchronous, partially synchronous, and asynchronous models, such as in Rethinking Large-Scale Consensus and PaLa: A Simple Partially Synchronous Blockchain.
[16] Later, as Ethereum moved from proof-of-work to proof-of-stake, a new consensus mechanism was utilized, known as Gasper, a combination of Casper the Friendly Finality Gadget (Casper-FFG) and the LMD-GHOST fork choice algorithm. I will not explain how Gasper works as it isn’t relevant to the essay.
[17] It’s important to note that a Tree is a restricted form of a graph and fits within the category of a DAG, utilizing the parent/child relationship. However, a child within a tree can only have one parent. A DAG, on the other hand, can have multiple parents (otherwise known as predecessors).
[18] Sompolinsky, Yonatan, et al. SPECTRE: Serialization of Proof-of-Work Events: Confirming Transactions via Recursive Elections, 2016, eprint.iacr.org/2016/1159.pdf
[19] Zohar, Aviv. SPECTRE: Serialization of Proof-of-Work Events, Confirming Transactions via Recursive Elections, 18 Dec. 2016, medium.com/blockchains-huji/the-spectre-protocol-7dbbebb707b5.
[20] Taken from the SPECTRE White Paper.
[21] Transitive means that if a < b and b < c, then a < c. However, there is a Condorcet paradox regarding SPECTRE allowing a < b, b < c, c < a to occur.
[22] Sompolinsky, Yonatan, Shai Wyborski, et al. PHANTOM GHOSTDAG A Scalable Generalization of Nakamoto Consensus, 10 Nov. 2021, eprint.iacr.org/2018/104.pdf
[23] Given a particular block, its selected parent is the parent with the highest blue score. The entire k-cluster is not calculated when a new block is created. Instead, most of the k-cluster is inherited from the block’s parent. Thus, a block tracks those in its blue past but not in its parent’s blue past. In this sense, GHOSTDAG creates a generalization of Nakamoto Consensus since by choosing K=0, the blue score is the length of the longest chain, and the selected chain is the original Nakamoto chain.
[24] “Cryptocurrency Milestone: Kaspa Hits Record 10 Blocks Per Second on Testnet, Redefines Proof-of-Work Speed Standards .” Digital Journal, 27 June 2023, www.digitaljournal.com/pr/news/binary news-network/cryptocurrency-milestone-kaspa-hits-record-10-blocks-p er-second-on-testnet-redefines-proof-of-work-speed-standards.
[25] In other words, implementing a hardwired bound on network latency.
Parameter K can be derived from D and L — and another parameter, delta, indicating how secure you want to be. In reality, GHOSTDAG is secure against 50%-delta attacks where delta is as small as you want, but K still grows (quadratically, not exponentially like in GHOST) with delta.
[26] Sutton, Michael, and Yonatan Sompolinsky. The DAG KNIGHT Protocol: A Parameterless Generalization of Nakamoto Consensus, 23 Feb. 2023, eprint.iacr.org/2022/1494.pdf
[27] Until DAGKNIGHT, only partially synchronous or asynchronous models were possible under a security threshold of 33% important, as shown by Rafael Pass and Elaine Shi. DAGKNIGHT is the first permissionless parameterless consensus protocol that is secure against attackers with less than 50% of the computational power in the network.
[28] Shai (Deshe) Wyborski confirmed the term PHANTOM-X via private correspondence.
[29] Taken from the DAGKNIGHT White Paper as recorded through simulations by the authors.
[30] A simulation of a network mining 𝜆 = 3.75 blocks per second and a secret attacker with 𝛼 = 0.2, the required risk parameter was set to 𝜖 = 0.05.
[31] However, if Bitcoin remains a store of value, then a different generalized Nakamoto Consensus cryptocurrency must prevail as a cryptocurrency intended to be used by the masses.
[32] Other BlockDAG variants include Meshcash — in Tortoise and Hares Consensus: the Meshcash Framework for Incentive-Compatible, Scalable Cryptocurrencies by Iddo Bentov, Pavel Hub’aˇcek, Tal Moran, and Asaf Nadler — and OHIE in OHIE: Blockchain Scaling Made Simple by Haifeng Yu, Ivica Nikolic, Ruomu Hou, and Prateek Saxena. Meshcash later adopted a new consensus mechanism, Spacemesh, which utilized proof-of-space instead of proof-of-work. Spacemesh was formulated in The Spacemesh Protocol: Tortoise and Hare Consensus… In… Space by Iddo Bentov, Julian Loss, Tal Moran, and Barak Shani.
Also see SoK: Consensus in the Age of Blockchains, by Shehar Ban, et al, for a history of Blockchain Consensus before GHOSTDAG.

[33] For the original OPOW paper, see Optical Proof of Work by Michael Dubrovsky, Marshall Ball, and Bogdan Penkovsky. For Stanford lab papers on OPOW, see LightHash: Experimental Evaluation of a Photonic Cryptocurrency by Sunil Pai, et al, and Experimental evaluation of digitally-verifiable photonic computing for blockchain and cryptocurrency, by Sunil Pai, et al.

[34] oPoW Resource Page, provided by PoWx, a Non-Profit organization, https://www.powx.org/opow.
[35] Lewenberg, Yoad, et al. “Bitcoin Mining Pools: A Cooperative Game Theoretic Analysis.” Proceedings of the 14th International Conference on Autonomous Agents and Multiagent Systems, 2015, https://www.ifaamas.org/Proceedings/aamas2015/aamas/p919.pdf.
